Im Gegensatz zu den Potenzfunktionen, bei denen die Basis die unabhängige Größe (Variable) und der Exponent fest vorgegeben ist, ist bei Exponentialfunktionen der Exponent (auch Hochzahl) des Potenzausdrucks die Variable und die Basis fest vorgegeben. Darauf bezieht sich auch die Namensgebung.Die e-Funktion besitzt keine Nullstellen. Sie schneidet die y-Achse an dem Punkt . Die natürliche Exponentialfunktion nimmt keine negativen Werte an. Ihre Umkehrfunktion ist die natürliche Logarithmusfunktion f – 1 ( x ) = ln x . und spiegeln sich an der Winkelhalbierenden.Eine Potenzfunktion ist eine Funktion, bei der die Variable die Basis einer Potenz ist. Der Exponent ist meistens eine Zahl oder kann eine konstante Variable sein, die meist mit n dargestellt wird. Die Variable x ist immer die Basis. Ist die Variable im Exponenten, handelt es sich um eine Exponentialfunktion.

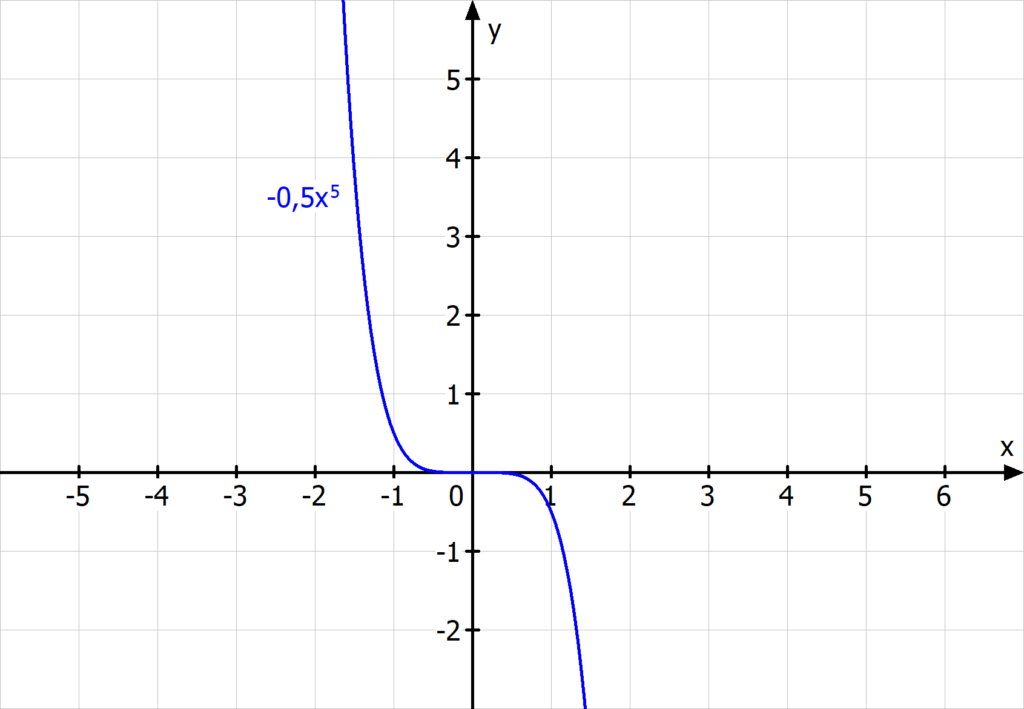
Wie erkenne ich eine Potenzfunktion : Eine Potenzfunktion f (mit natürlichem Exponenten) ist eine Funktion mit einem Funktionsterm der Form f(x)=xn . Die natürliche Zahl n ist der Grad der Potenzfunktion, man spricht auch von einer Potenzfunktion vom Grad n . Eine allgemeine Potenzfunktion f hat einen Funktionsterm der Form f(x)=axn .

Was ist das Besondere an Exponentialfunktionen

Eigenschaften der Exponentialfunktion

Exponentialfunktionen haben also keine Nullstelle. Die Funktionswerte nähern sich aber beliebig dicht der Null an. Die x-Achse bzw. die Gerade y=0ist die waagerechte Asymptoteder Exponentialfunktion.

Wie lautet die Exponentialfunktion : Die allgemeine Exponentialfunktion lautet f ( x ) = a ⋅ b x . Es kann vorkommen, dass die Funktionsgleichung noch den Parameter d enthält, welcher den Funktionsgraphen in y-Richtung verschiebt. Der Parameter gibt den y-Achsenabschnitt an, kann aber durch den Parameter d verändert werden.

Die allgemeine Exponentialfunktion lautet f ( x ) = a ⋅ b x . Es kann vorkommen, dass die Funktionsgleichung noch den Parameter d enthält, welcher den Funktionsgraphen in y-Richtung verschiebt. Der Parameter gibt den y-Achsenabschnitt an, kann aber durch den Parameter d verändert werden.

Inhalt: Die Exponentialfunktion dient zur Beschreibung von extremem Wachstum und Zerfall. Die Variable steht im Exponenten.

Was sind die Eigenschaften von Potenzfunktionen

Die Graphen von Potenzfunktionen haben charakteristische Eigenschaften, die oft davon abhängen, ob die Hochzahl n gerade oder ungerade ist.

• Wertemenge: n gerade: keine negativen Zahlen.
• Symmetrie: n gerade: Achsensymmetrie zur y-Achse.
• Vorfaktor a. Der Wert des Parameters a ist der Funktionswert an der Stelle x = 1.

Eine Exponentialfunktion lässt sich auch allgemein durch die Formel f(x)=b⋅ac⋅x+d+e darstellen.Die Exponentialfunktion ist nach der Form f(x)=a*bx aufgebaut, während die Potenzfunktion die Form f(x)=a*xn hat. Beispiele für ein exponentielles Wachstum sind Epidemien oder die Ausbreitung des Corona-Virus in 2020. Bei dieser hat sich die Anzahl der Infizierten alle paar Tage verdoppelt.

Eigenschaften

• f(x) = a^x.
• Die Variable (x) steht im Exponenten.
• Exponentialfunktionen sind Funktionen der Form f(x)=ax, wobei a eine positive reelle Zahl ungleich 1 und x eine beliebige reelle Zahl ist.
• Die Basis der Exponentialfunktion ist größer als 0 und kleiner als 1.

Was gilt für jede Potenzfunktion : Symmetrien bei Potenzfunktionen

Eine allgemeine Potenzfunktionf mit gerademGrad ist eine geradeFunktion. Es gilt f(x)=f(-x)für alle reellen Zahlen x. Jeder Punkt x | f x wird bei Spiegelung an der y-Achse auf den Punkt – x | f x abgebildet.

Was sind Exponentialfunktionen Beispiele : Die Exponentialfunktion ist nach der Form f(x)=a*bx aufgebaut, während die Potenzfunktion die Form f(x)=a*xn hat. Beispiele für ein exponentielles Wachstum sind Epidemien oder die Ausbreitung des Corona-Virus in 2020. Bei dieser hat sich die Anzahl der Infizierten alle paar Tage verdoppelt.

Welche Arten von Potenzfunktionen gibt es

Unbenannte Notiz – Das Wichtigste

	Gerader Exponent	Ungerader Exponent
Positiver Exponent	Parabel – achsensymmetrisch zur -Achse	Parabel – punktsymmetrisch zum Ursprung
Negativer Exponent	Hyperbel – achsensymmetrisch zur -Achse	Hyperbel – punktsymmetrisch zum Ursprung