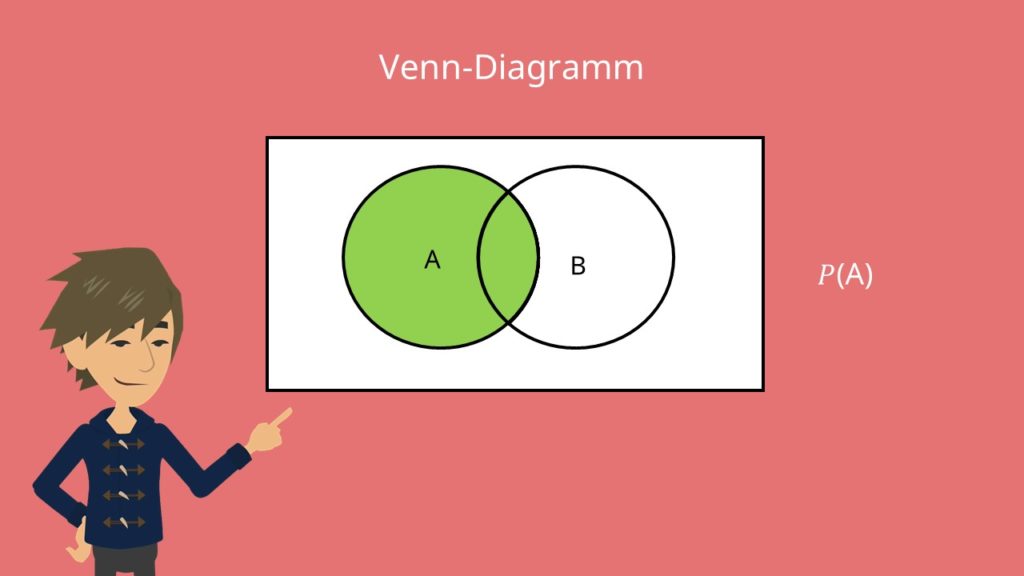
Die Wahrscheinlichkeit (auf Englisch probability) ist also ein Maß, das bestimmt wie sehr erwartet wird, dass genau dieses Ereignis eintritt. Mathematisch geschrieben wird die Wahrscheinlichkeit des Ereignisses X ausgedrückt als P(X). Sie kann Werte im Bereich zwischen [0,1] annehmen.Eine Wahrscheinlichkeitsverteilung oder Wahrscheinlichkeitsfunktion einer Zufallsgröße ist eine Funktion, die jedem Wert xi einer Zufallsgröße X eine Wahrscheinlichkeit P(X=xi) zuordnet.Um diesen Einfluss zu untersuchen, wird der Begriff der bedingten Wahrscheinlichkeit eingeführt: P B ( A ) ist die Wahrscheinlichkeit von unter der Bedingung, dass eingetreten ist. Statt P B ( A ) schreibt man auch häufig P ( A | B ) .

Ist die relative Häufigkeit die bedingte Wahrscheinlichkeit : Das Gesetz der großen Zahl besagt, dass eine Abschätzung der Wahrscheinlichkeit als relative Häufigkeit immer genauer wird, je größer die Stichprobe ist. Eine bedingte Wahrscheinlichkeit gibt an, wie wahrscheinlich Ereignis A ist, wenn man schon weiß, dass ein anderes Ereignis B eingetreten ist.

Wie erkenne ich eine bedingte Wahrscheinlichkeit

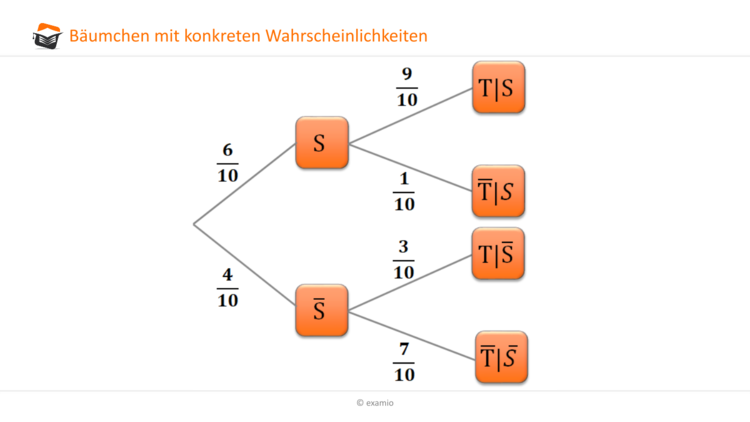
Die bedingte Wahrscheinlichkeit wird berechnet, indem man die Wahrscheinlichkeit des gemeinsamen Eintretens von zwei Ereignissen durch die Wahrscheinlichkeit des gegebenen Ereignisses teilt. Die Formel lautet P(A|B) = P(A ∩ B) / P(B), wobei P(A|B) die Wahrscheinlichkeit von A unter der Bedingung B ist.

Wann liegt eine bedingte Wahrscheinlichkeit vor : Als bedingte Wahrscheinlichkeit des Ereignisses A unter der Bedingung B bezeichnet man P B ( A ) = P ( A ∩ B ) P ( B ) , falls P ( B ) ≠ 0 gilt.

Um eine Wahrscheinlichkeit zu definieren, gibt es verschiedene Möglichkeite:

• klassischer Wahrscheinlichkeitsbegriff,
• axiomatischer Wahrscheinlichkeitsbegriff (= Kolmogoroffscher Wahrscheinlichkeitsbegriff),
• statistischer Wahrscheinlichkeitsbegriff,
• subjektiver Wahrscheinlichkeitsbegriff.

Die Wahrscheinlichkeitsverteilung wird in zwei Arten unterteilt, die diskrete und die stetige Zufallsvariable.

Wie berechnet man die bedingte Wahrscheinlichkeit

Wie wird Bedingte Wahrscheinlichkeit berechnet Die Berechnung der bedingten Wahrscheinlichkeit basiert auf der Erinnerung an die Formel für die bedingte Wahrscheinlichkeit, die lautet P ( A | B ) = P ( A ∩ B ) P ( B ) , vorausgesetzt P ( B ) > 0 .Die unbedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit, dass ein Ereignis eintritt, ohne dass davon ausgegangen wird, dass ein anderes Ereignis eingetreten ist, während die bedingte Wahrscheinlichkeit die Wahrscheinlichkeit ist, dass ein Ereignis eintritt, gegeben, dass ein anderes Ereignis bereits eingetreten …Regeln Wahrscheinlichkeitsrechnung

Regel	Formel	Erklärung
Multiplikationsregel für unabhängige Ereignisse	P ( A und B ) ≡ P ( A ∩ B ) ≡ P ( A ∧ B ) = P ( A ) ⋅ P ( B )	Die Wahrscheinlichkeit, dass zwei unabhängige Ergebnisse auftreten, entspricht dem Produkt der jeweiligen Wahrscheinlichkeiten.

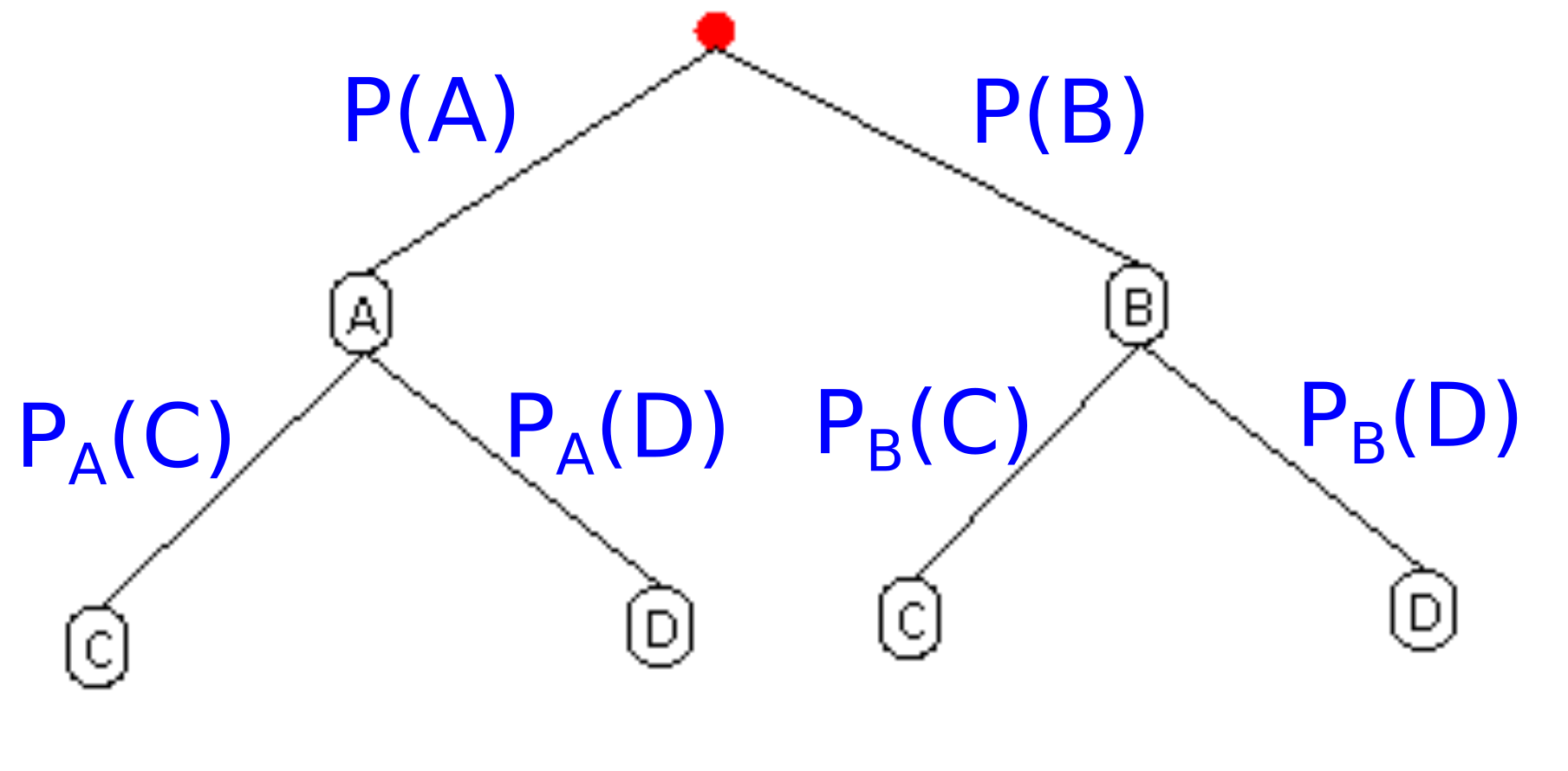
auch nur mithilfe des Baumdiagramms lösen kann. Auf den unteren Stufen eines Baumdiagramms stehen sogenannte bedingte Wahrscheinlichkeiten. „Wie groß ist die Wahrscheinlichkeit, dass Ereignis C eintritt, wenn wir bereits wissen, dass Ereignis A eintritt “

Wie kann man die Wahrscheinlichkeit bestimmen : Wie berechne ich die Wahrscheinlichkeit Die Wahrscheinlichkeit berechnest Du, indem Du die Anzahl der günstigen Fälle durch die Anzahl der möglichen Fälle teilst.

Was für Wahrscheinlichkeiten gibt es : Um eine Wahrscheinlichkeit zu definieren, gibt es verschiedene Möglichkeite:

• klassischer Wahrscheinlichkeitsbegriff,
• axiomatischer Wahrscheinlichkeitsbegriff (= Kolmogoroffscher Wahrscheinlichkeitsbegriff),
• statistischer Wahrscheinlichkeitsbegriff,
• subjektiver Wahrscheinlichkeitsbegriff.

Welche Arten von Wahrscheinlichkeit gibt es

Um eine Wahrscheinlichkeit zu definieren, gibt es verschiedene Möglichkeite:

• klassischer Wahrscheinlichkeitsbegriff,
• axiomatischer Wahrscheinlichkeitsbegriff (= Kolmogoroffscher Wahrscheinlichkeitsbegriff),
• statistischer Wahrscheinlichkeitsbegriff,
• subjektiver Wahrscheinlichkeitsbegriff.

Um bei einem Wurf die Summe zwei zu erhalten, müssen Sie zwei Einsen werfen. Da diese Kombi- nation nur einmal vorkommen kann, beträgt die Wahrscheinlichkeit, die Summe Zwei zu erhalten: 1/36. Die Wahrscheinlichkeit, die Summe drei zu werfen, beträgt 2/36, weil nur zwei Ergebnisse diese Summe ergeben: 1-2 oder 2-1.