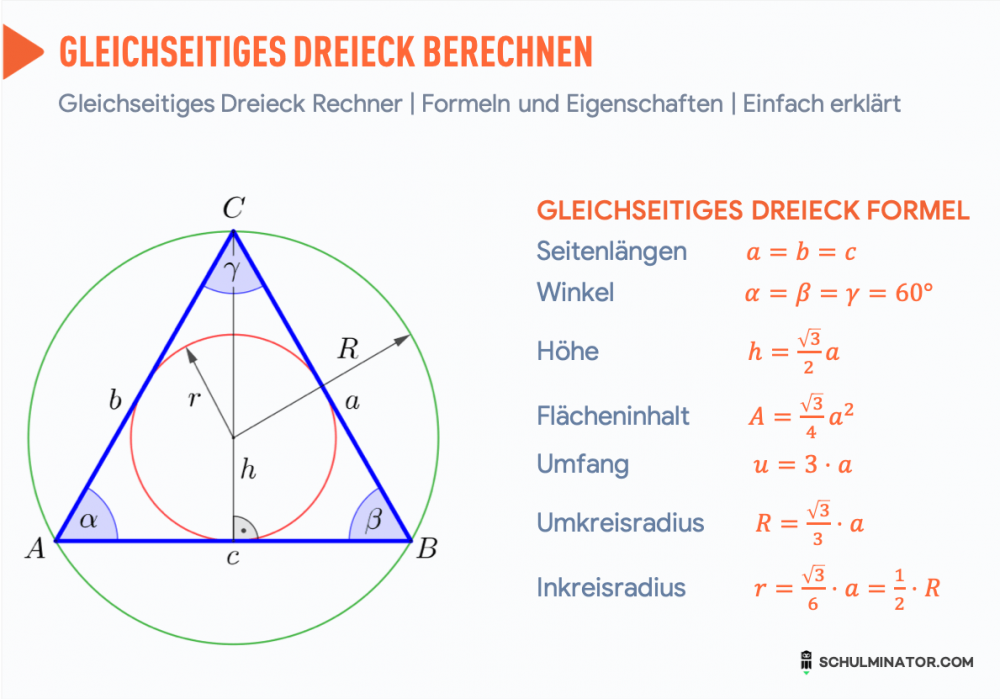
Welche Formeln gibt es zu einem Gleichseitiges Dreieck Standardformeln: Fläche: A= a2⋅√34. Umfang: U= 3⋅a.Den Flächeninhalt eines Dreiecks berechnest du so: Grundseite mal Höhe dividiert durch zwei. Sieh dir dazu die Grafik noch einmal genau an!Wie der Name schon verrät, sind beim gleichseitigen Dreieck alle Seiten gleich lang. Es hat aber noch mehr Besonderheiten. Alle Innenwinkel in diesem Dreieck sind gleich 60°. Alle Seiten a = b = c sind im gleichseitigen Dreieck gleich lang.

Wie berechnet man die Fläche von einem gleichschenkligen Dreieck : Wie berechnet man den Flächeninhalt von einem gleichschenkligen Dreieck So berechnest du Fläche und Umfang von einem gleichschenkligen Dreieck: Umfang: U = 2 ⋅ a + c. Fläche: A = 0,5 ⋅ c ⋅ h.

Wie groß ist die Fläche eines gleichseitigen Dreiecks mit Seiten

In einem gleichseitigen Dreieck sind Median, Winkelhalbierende und Höhe für alle Seiten gleich und sind die Symmetrielinien des gleichseitigen Dreiecks. Die Fläche eines gleichseitigen Dreiecks beträgt √3 a 2 / 4 .

Wie groß ist die Fläche eines gleichseitigen Dreiecks mit einer Innenhöhe von 55 cm und einer Grundlänge von 75 cm : Die Fläche des Dreiecks beträgt 2062,50 cm² .

Ein gleichseitiges Dreieck mit einer Innenhöhe von 55 cm und einer Basislänge von 75 cm.

Der Flächeninhalt eines Rechtecks berechnet sich mit der Formel: A = a · b. Da man zwei Längeneinheiten multipliziert, erhält man immer eine Flächeneinheit, z.B.: cm · cm=cm2 (Man sagt: Quadratzentimeter) m · m=m2 (Man sagt: Quadratmeter)

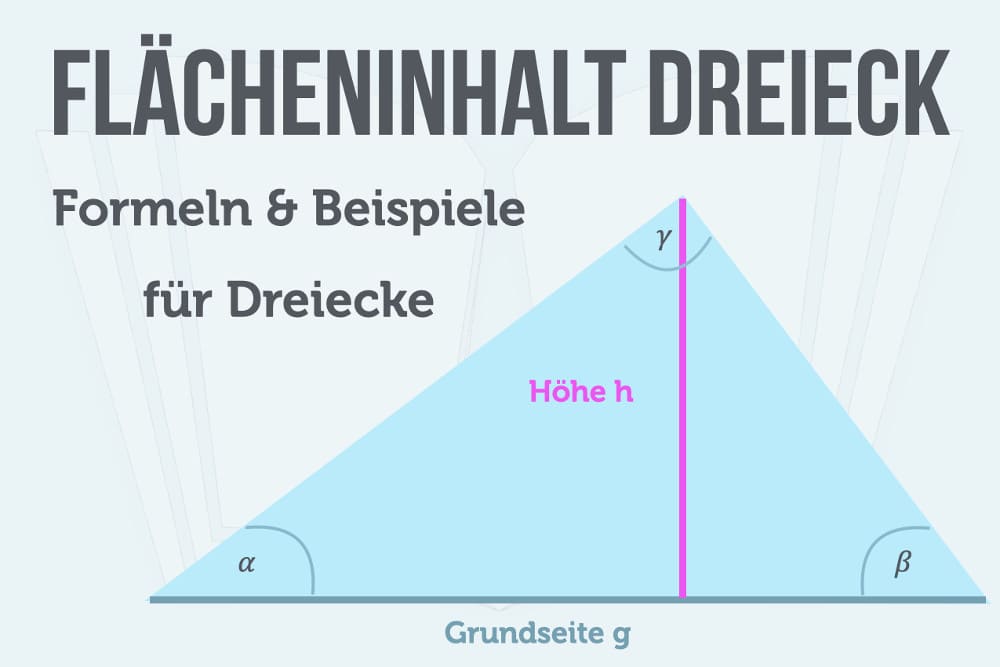
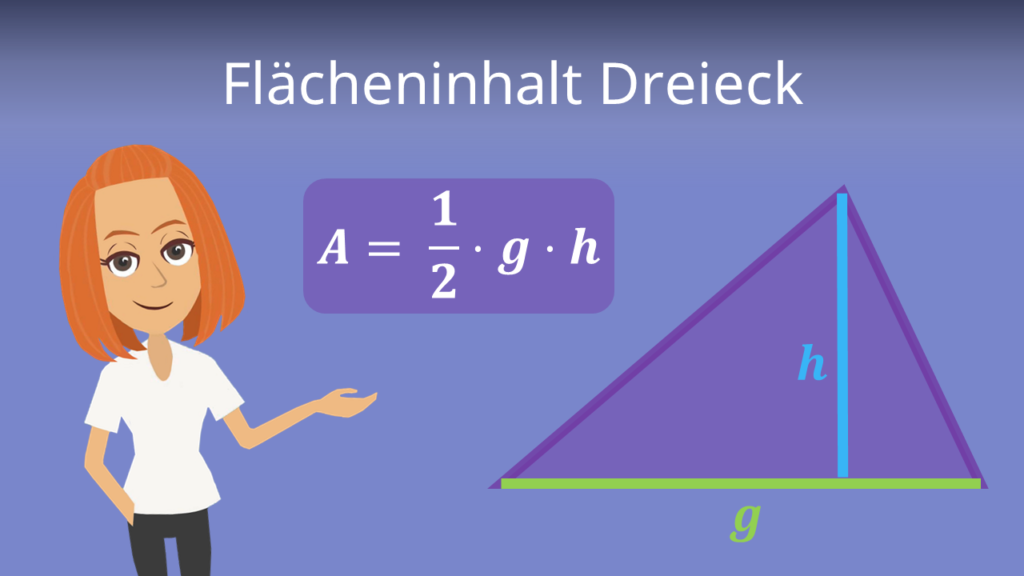
Um den Flächeninhalt eines Dreiecks zu berechnen, kannst du je nachdem, welche Werte du gegeben hast, die allgemeine Formel für den Flächeninhalt (A = 1/2 * g * h) oder die Formel für zwei gegeben Seiten und deren Innenwinkel (A = (a * b * sin(alpha)) / 2) verwenden.

Wie kann man beweisen, dass ein Dreieck ein gleichseitiges Dreieck ist

Antwort: Wenn drei Seiten eines Dreiecks gleich sind und das Maß aller drei Winkel 60 Grad beträgt, dann ist das Dreieck ein gleichseitiges Dreieck.Gleichseitiges Dreieck berechnen

• Bei einem gleichseitiges Dreieck sind alle drei Seiten gleich lang und die Winkel betragen alle genau 60 °.
• Im gleichseitigen Dreieck sind immer alle Winkel gleich groß.
• Gleichseitiges Dreieck Symmetrie.

Flächeninhalt eines Dreiecks berechnen

Den Flächeninhalt eines rechtwinkligen Dreiecks (A) berechnest du, indem du die Längen der Seiten, die den rechten Winkel einschließen, multiplizierst: A=12a·b, wobei a und b die Längen der Seiten, die den rechten Winkel einschließen, bezeichnen.

Daher beträgt die Fläche eines gleichseitigen Dreiecks 5,196 cm2 .

Wie groß ist die Fläche eines gleichseitigen Dreiecks, dessen Seiten 8 cm lang sind : 16√3 cm2 .

Wie finde ich die Fläche eines gleichseitigen Dreiecks ohne Höhe : Schritt 1: Notieren Sie sich das Maß der Seitenlänge des gleichseitigen Dreiecks. Schritt 2: Wenden Sie die Formel an, um die Fläche des gleichseitigen Dreiecks wie folgt zu berechnen: A = (√3/4)a 2 , wobei a das Maß für die Seitenlänge des gleichseitigen Dreiecks ist. Schritt 3: Drücken Sie die Antwort mit der entsprechenden Einheit aus.

Wie groß ist die Fläche eines gleichseitigen Dreiecks mit einer Seitenlänge von 2 cm

The required area is √3 .

We are given that the side is 2 cm.

Die Fläche berechnet sich meist aus Länge mal Breite. z.B.: Für die Fläche eines Gartens nimmst du gewöhnlich Länge mal Breite, damit herausfinden kannst, wie viel Quadratmeter Saat du bestellen musst. Für den Umfang zählst Du alle Seiten, der Figur, zusammen.5:10Empfohlener Clip · 56 Sekunden

Wie finde ich die Fläche eines Dreiecks ohne Basis : Die Seiten der Beine müssen gleich sein, also quadrieren Sie einfach die Länge eines der Beine und dividieren durch 2 . Wenn Sie nur die Hypotenuse haben: Da gleichschenklige rechtwinklige Dreiecke im Verhältnis 1-1-(Quadratwurzel aus 2) vorliegen, dividieren Sie einfach die Hypotenuse durch sqrt(2), quadrieren das Ergebnis und dividieren durch 2.